欧拉常数与圆周率
e 是一个不可思议且特别的定数。在这层意义上,欧拉常数 e 与圆周率 π 是两个至关重要的数学定数,就算说成是神赐予人类的数字也不为过。吹爆炸!!!
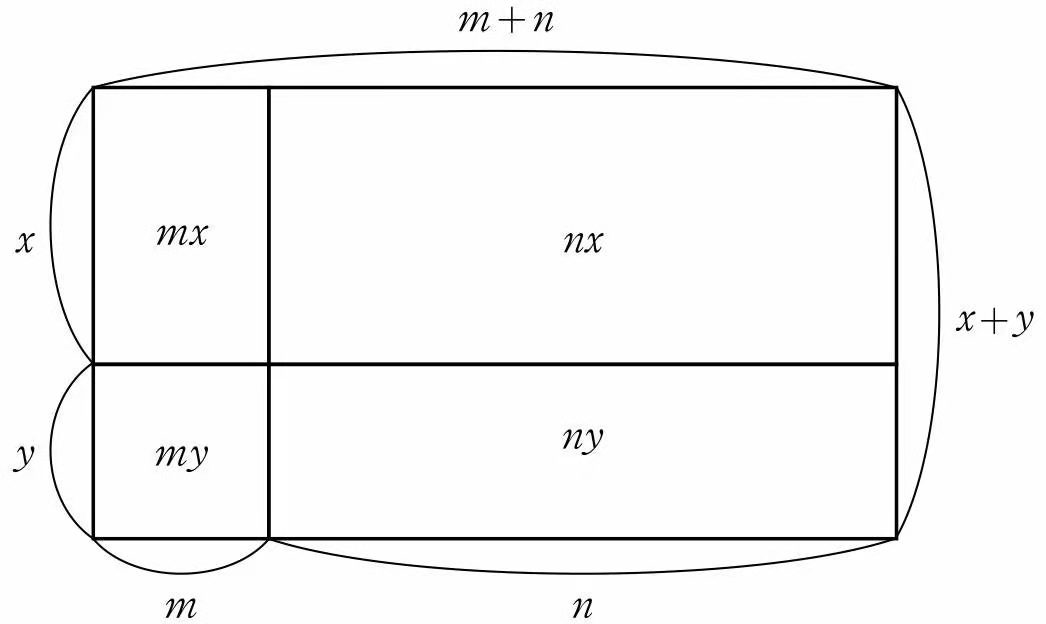
(m+n)(x+y) = mx + my + nx + ny
除法的两个意义
a÷n=p
等分除
将a分成n等份,则每份有p个。不同单位的比例为等分除。
包含除
将a按照每份有n个等分,则可以分成p份(a有p份的n个)。相同单位的比例为包含除。
图表的特点
- 柱状图:表示大小
- 折线图:表示变化
- 饼图:表示比例
- 带状图:比较比例
频数分布表
频数分布表就是将每组中的频数、相对频数、累计相对频数等做成一张表。
- 组:将数据以相同间隔分开的区间。
- 组中值:各组上下限中间的数值。
- 频数:各组中包含数值的数量。
- 相对频数:各组数据频数在总频数中的占比。
- 累计相对频数:逐级相对频数相加的和。
分组取组段值
分组取组段值时,可以参照下面的JIS(日本工业标准的简称)标准:
将包含最大值与最小值在内的数据,分成5~20组时,用最大值与最小值之差(R)除以1、2、5(或者是10、20、50;0.1、0.2、0.5)等各备选范围,选择结果在5~20范围内的数。如果有两个不同的结果,那么,最大值与最小值之差大于100则取小,反之则取大。
中位数
将数据由大到小排列时,位于最中间的数值。
中位数的求法
- 将数据按大小排列。
- “当数据个数为奇数时”:中位数=正中间的数值。
- “当数据个数为偶数时”:中位数=正中间两个数值的平均值。
众数
一组数据中出现次数最多的数值。即频数最高的数据的值。
偏差
偏差 = 50 + (指定的值-平均值)/标准差 * 10
四分位数
四分位数是指,将数据从小到大排列并分成4等份后,处于3个分割点上的数。这3个四分位数按照从小到大的顺序分别被称为第一四分位数、第二四分位数和第三四分位数。
第二四分位数和数据的中位数是一致的。
四分位数的求法
- 找出数据的最大值与最小值。
- 找出数据的中位数→第二四分位数。
- 求出中位数前半部分数据的中位数→第一四分位数。
- 求出中位数后半部分数据的中位数→第三四分位数。
倍数的辨别方法
2的倍数:尾数为偶数。
3的倍数:各位数相加的和为3的倍数。
4的倍数:末尾两位数为4的倍数或整百数。
5的倍数:尾数为0或5。
6的倍数:尾数为偶数,且各位数的和为3的倍数。
7的倍数:将个位数字去掉之后的数 - 个位数字的两倍 = 7的倍数。
证明判断3的倍数方法
首先,拿一个3位数举个栗子,a,b,c 是一个小于10的正整数,则 100a + 10b + c可以表示一个三位数,从而可以得到 100a + 10b + c = 99a + 9b + (a + b + c),从而只需要各位数相加的和为3的倍数即可。更多位数同理可证。
证明判断7的倍数方法
如果把一个数记作 10x + y,则10x + y = 7(x + y) + 3x - 6y = 7(x + y) + 3(x - 2y),即将个位数字去掉之后的数 - 个位数字的两倍=7的倍数。
二项分布
一般来说,成功概率为p的实验,独立重复n次后的成功次数为X的概率分布,被称为关于发生概率为p、次数为n的二项分布。
和事件与积事件
一般来说,如果一个试验中有A与B两个事件,“A与B至少有一个事件发生”的事件被称为A与B的和事件,写作A∪B;而“A与B同时发生”的事件被称为积事件,写作A∩B。