证明杂记

发表于 | 更新于 | 分类于 ， | 阅读次数：
本文字数： 1.1k | 阅读时长 ≈ 1 分钟

如何证明 0.99999…… = 1

方法一

1/3 = 0.33333…… ==> 1 = 0.99999……

方法二

10 * 0.99999…… = 9.9999……
两边各减去一个 0.99999…… ==> 9 * 0.99999…… = 9 ==> 0.99999…… = 1

方法三

0.99999…… = 0.9 + 0.09 + 0.009 + ……
采用等比数列求和，然后求极限。

从而可以得到 0.99999…… + n = n + 1，例如： 9.99999…… = 10

有趣的 PI 和 E

1
2
3
4
> Math.pow(Math.PI, 4) + Math.pow(Math.PI, 5)
403.4287758192838
> Math.pow(Math.E, 6)
403.428793492735

PI^4 + PI^5 约等于 E^6 可以精确到小数点后四位。
紧跟这个精度之后的是 PI^146 + PI^152 约等于 E^174

1
2
3
4
> Math.pow(Math.PI, 146) + Math.pow(Math.PI, 152)
3.6917488742520865e+75
> Math.pow(Math.E, 174)
3.6918143295804325e+75

神奇！神奇！神奇！
有趣！有趣！有趣！

时间复利

1
2
3
4
> Math.pow((1+1/365), 365)
2.714567482021973
> Math.pow((1+1/365), 365*10)
21727.333146076744

二次方程的替代解法

  1. 如果找到两个数r和s，它们的和为-B、乘积为C，那么 x^2 + Bx + C = (x - r)*(x - s) 成立，且 r 和 s 即为该方程的根。
  2. 当两个数字分别为 -B/2 + u 和 -B/2 - u 时，两数之和为-B。
  3. 由1可知，两数乘积为C, 所以两个数字相乘得出 B^2/4 - u^2 = C 。
  4. 开平方运算后，满足上述条件的 u 一定存在。
  5. 所以 -B/2 + u 和 -B/2 - u 分别代表 r 和 s ，是该方程全部的根。

第1点于数百年前已知 （因式分解、韦达定理逆定理）。第2、3、4点被发现于数千年前（古巴比伦人、古希腊人）。

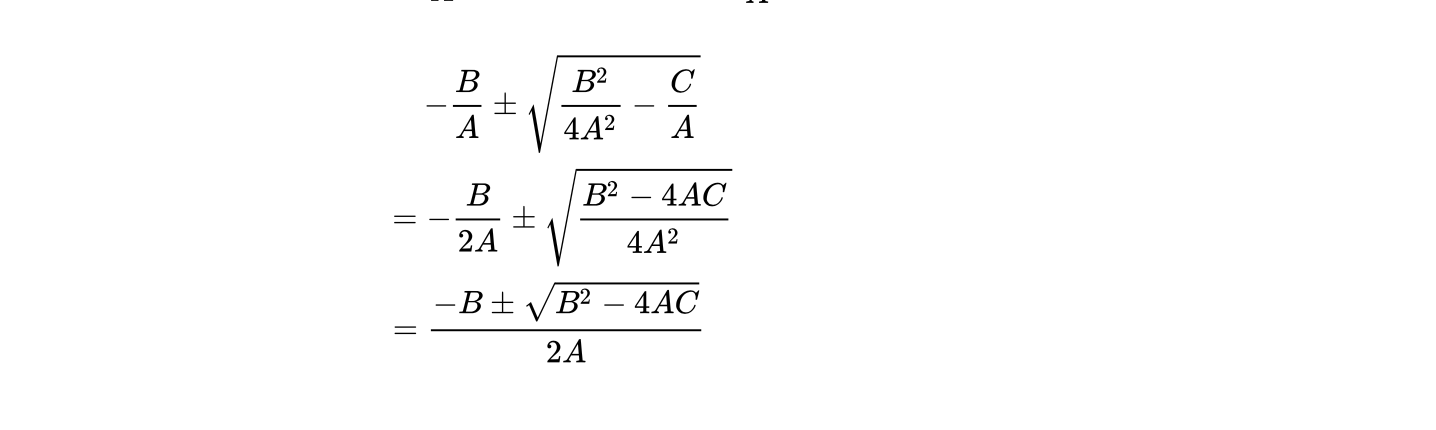
所以由 Axx + Bx + C = 0 可以得出 xx + (B/A)^2*x + C/A = 0;

然后，按照上面的方法，把 B/A 插入 B 的位置，C/A 插入 C 的位置，便可以得出如下公式：