在一个8×8的国际象棋棋盘上, 显然我们可以用32张多米诺骨牌覆盖整个棋盘上的64个方格。
问:如果将对角线上的两个方格挖掉, 那剩下来的62个格子还能用31张骨牌覆盖住吗?

答:每一张骨牌在棋盘上必是覆盖住两个相邻方格, 一白一黑。挖掉两个角之后只有 32 黑 30 白, 于是就不存在这样一种能用31个骨牌覆盖的方法。
问:任意切掉一个一白一黑的格子就一定可以吗?
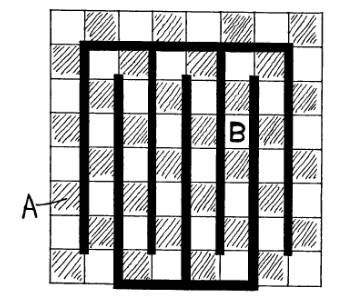
答:可以。粗黑线条将整个棋盘转变为一条首尾相连、黑白格相间的封闭路线。从这棋盘上切掉任何两个颜色不同的方格, 会让这个封闭线路变成两段线路, 当然如果切掉的方格是相连的, 那就是一条线路。显然, 在任何线路中, 两种颜色的格子数量都是偶数,故分别都可以被若干张骨牌覆盖。从而整个棋盘一定可以被31张骨牌完全覆盖。